
Fast Methods for Geometric Inference in Limited‐Angle Tomography

Project #: 22-137 | Year 3 of 3
Sean Breckling,a Christian Bombara,a,b Jordan Pillow,a Malena Españolc
aNevada National Security Site (NNSS), bYale University, cArizona State University
Executive Summary
We are developing and implementing novel techniques to accurately quantify 3D volumetric density from an extremely limited number of X-ray projection images. This work was motivated, in part, by open questions regarding uncertainties inherent in assuming a perfect radial symmetry of hydrodynamic dynamic scenes.
Description
Single and extremely few-view (EFV) X-ray imaging modalities are the most common techniques used to reconstruct data from dynamic experiments. In the single-view reconstructions, it is assumed that the 3D volumetric density of the target region enjoys a perfect radial symmetry; however, data rarely support this assumption. This condition makes us question how much 3D geometric information is available in imaging applications where as few as one or two projection angles are recorded. Can we use that information to mitigate these resulting geometric uncertainties directly or implicitly? If so, to what extent? We suspect that recent developments in extremely few–view tomographic reconstruction techniques stand to improve our analyses and our uncertainty quantification capability.
The bulk of major developments seen in single view, limited-angle, and few-view tomographic reconstruction methodologies in recent years have been seen as improvements to modeling and numerical optimization. In year three, both avenues were explored for the single-view (Abel 1826), EFV, and a new combination of single-view X-ray radiography and photo doppler velocimetry (PDV) momentum-diagnostic modalities. These efforts have produced several prototype algorithm implementations that need only to be tuned to an NNSS testbed for use.
The standard model for regularized CT reconstruction seeks to reconstruct a volumeuwhich minimizes a loss function of the form
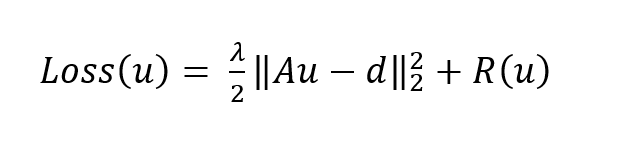
via numerical optimization. The operatorA is the forward projection model,dis the radiography data, andR(u)is a non-negative regularization penalty. In year three, we developed new capabilities to solve Equation 1, when the forward model is in one of the three of the following forms:
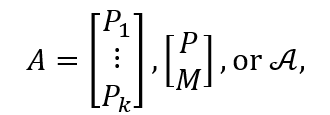
where operators P denote classic Radon projection operators from a single k-indexed vantage point. The operator M also denotes the Radon transform, but specifically from the momentum diagnostic’s vantage. Lastly, A specifies the axially symmetric transform (Abel Transform, if the vantage is idealized.)
During the summer months, several numerical optimization approaches were used to solve the EFV model, with two views in the Cygnus configuration (60 degrees between the vantages) and the DARHT configuration (90 degrees). These results will be discussed at length in the final report.
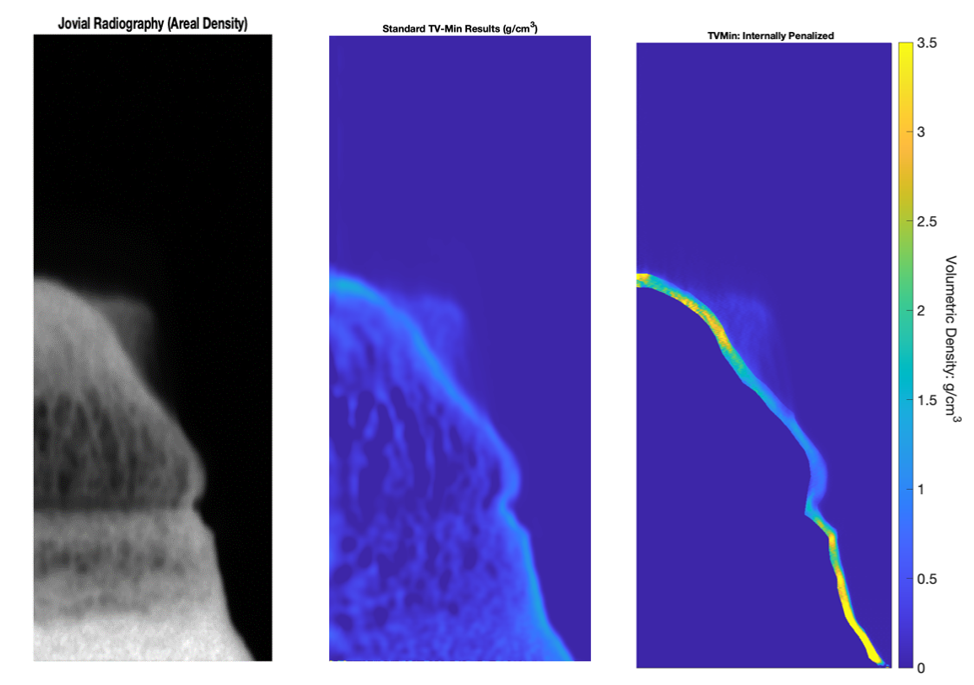
The Jovial series at the NNSS’s Special Technologies Laboratory’s Boom Box provided an opportunity to combine well-characterized radiography of a hydrodynamic scene with a momentum diagnostic capable of measuring mass in ranges that span much of the material seen in the radiographic field of view. It is presumed and cross-verified using PDV that the bulk of the mass is contained within the surface near the front of the wave. However, from the perspective of the radiography, seen in Figure 1 below, we see striations on the surface of the propelled coupon surface. The standard axial symmetry model used in single-view reconstruction methods will fail to correctly place volumetric density at that surface region, instead filling up much of the internal bubble with errant mass.
Among the numerous methods explored during FY22, we developed two alternative approaches to solving Equation 1 when an operator of type A is presumed by amending the regularization penalty with additional terms, e.g.
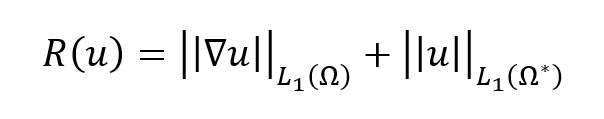
where Ω* ⊂ Ω is the presumed-empty internal volumetric region. An example result of this technique is seen on the right in Figure 1. More analysis will be required before this prototype technique is ready for publication or deployment on NNSS testbeds.
Conclusion
The largest success of the FY 2022 period spurred from the arrival of the combined Jovial radiography and Asay window velocimetry data. This sparked a substantial modelling effort during half of FY 2022. Given the novelty of the measurement configuration, the reconstruction modeling efforts were high-risk, but have proven to be a fruitful avenue for both a brand-new analytical capability, and new mathematics. This work will continue development under the Nimble series. Much of the limited-angle/EFV tomographic reconstruction efforts that began during FY 2021 continued into FY 2022. This includes two Alternating-Direction Method of Multipliers techniques to solve Equation 1, namely when
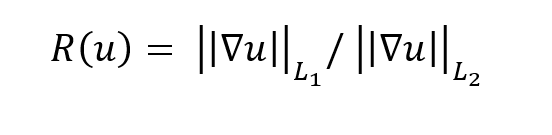
the physical relevance of tomographic reconstructions. This work has led to a publishable manuscript that is in a mature preprint stage.
Mission Benefit
The semi-blind deconvolution technique explored in FY 2021 through mid-year FY22 has proven quite fruitful. This image restoration methodology has been effective at estimating the so-called “Monty Wood” blurring kernel without the need for a rollbar in the field of view. A publishable report on this work, coauthored by Sean Breckling and Malena Español at ASU, is also in a mature preprint stage. Analysts working on the Stockpile Stewardship Data Analysis program will likely explore an extension of this work to produce anode spot reconstructions using a similar statistical learning strategy. Such a tool would represent a substantial new capability at any pulse-powered X-ray imaging testbed.
Publications, Technology Abstracts, Presentations/Posters
Breckling, S., M. I. Español, V. Uribe, C. Bombera, J. Pillow, B. Baldonado. 2023. “Box-Constrained L1/L2 Minimization in Single-View Tomographic Reconstruction.” arXiv: 2303.08292. https://doi.org/10.48550/arXiv.2303.08292.
References
Abel, N. H. 1826. “Auflösung einer Mechanischen Aufgabe.” Journal für die Reine und Angewandte Mathematik,1: 153–157. http://eudml.org/doc/183021.
This work was done by Mission Support and Test Services, LLC, under Contract No. DE-NA0003624 with the U.S. Department of Energy. DOE/NV/03624–1653.
Return to Radiographic Systems Imaging and Analysis
Go to SDRD Annual Report Index
Return to SDRD Homepage
